MTT's - Chip ramble vs ICM, giver det mening?

Nu har jeg brugt en del tid på at lege, med netop de her spots, beregningerne, og prøve at finde hoved og hale i hvornår vi kan og ikke kan bruge dem, og i hvor bred en forstand, jeg er med på at på et FT, hvor money jumps er ret relevante vil vi måske ikke gøre det? Men føler at +chip ev, gør at jeg alligevel føler vi kan. Klart var vi kun lige kommet ITM, så var det her et snap shove. 

Den aktuelle hånd: FT 180m SNG, 5 vejs, med 2 recs, 2 regs, og mig som er totalt MTT blank. 

No Limit Holdem Tournament

PokerStars

5 Players

Hand Conversion Powered by WeakTight Poker Hand History Converter

$2.28

Stacks:

UTG inde02 (111k) 37bb

CO Woodlin452 (42k) 14bb

BTN uill_mvp (65k) 22bb

SB Hero (32k) 11bb

BB MrDanielEdge (20k) 7bb

Blinds: 1.5k/3k Ante 300

Pre-Flop: (6k, 5 players) Hero is SB 9♠ 8♠

2 folds, uill_mvp raises to 6.6k, Hero ?

Final Pot: 13k

uill_mvp wins 13k (net +5.7k)

 

Afspil hånd

Skurk er en default spiller med en fornuftig høj åbnings frekvens her ~50%. 

Mine tanker går på at population overfolder, i spots hvor de spiller for ''store'' dele af deres stack (iE hvis jeg jammer, så skal han ud med 11bb af hans 22bb, og går fra en komfortabel position til at være short.). 

Lad os holde fast i at han raiser 50% her, og kalder af med top 16% - Så ser hans range således ud: 

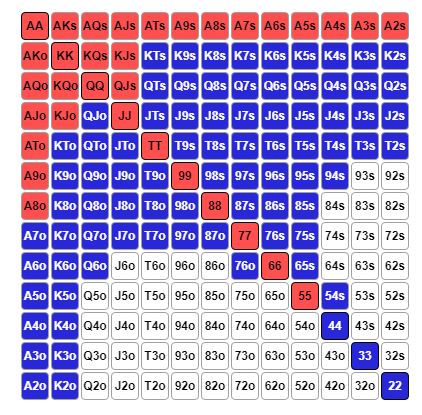
Og tror egentlig det er for wide en ralling range, for rigtig mange i de her SNG's (for den sags skyld i MTT's generalt, medmindre det er solide regs, efter hvad jeg føler jeg har mødt so faar). 

Vi har så også BB i potten, som dog må forventes hvis vi jammer, at have en absurd snæver range, og kun kalder top ~7% af hans range: 

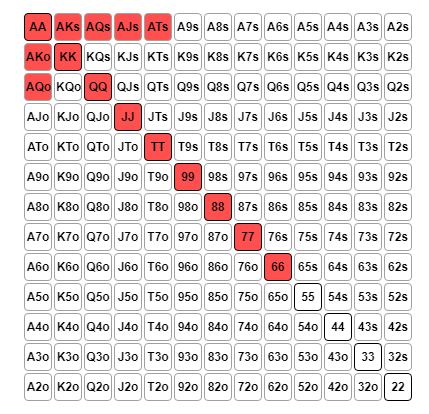
Ser vi så på matematikken uden ICM, har vi et spot der ser ud som følgende: 

Btn kalder altså ca 25% af hans range og folder 75%, imens BB kalder ca 7% af tiden. Altså vil vi se Calls 25 + 7 = 32% af tiden, og dermed folds 68% af tiden. 

Vores equity imod Btn når kaldt er 37%, vores equity imod BB er 33%. 

Formlen som jeg forstår det for at finde chip value er: 
Profit = 0.68 * 12600 + 0.25 * (0.37 * (31300 + 3000 + 1500 + 31300) - 29800) + 0.07 * (0.33 * (31300 + 3000 + 1500 + 31300) -29800)
Profit = 8568 + (-1243) + (-536)

Profit = +6789 chips, altså næsten +2.26bb on average på et shove.  

men antager vi at BB folder ud 97.5% og kun kalder QQ+ AKo+ AQs+, samt vi tilpasser Btn calling lidt til mine tanker om population (de fleste er nits i calls):

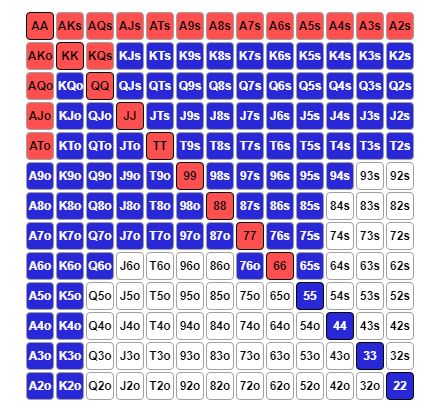
Så bliver formlen lidt anerledes, da de nu kun kalder 20% og 2.5%, altså får vi calls 22.5% og folds 77.5%, samt vores equity er således:
Equity vs Btn: 36.5% 
Equity vs BB: 31% 
Profit = 0.775 * 12600 + 0.20 * (0.365 * (31300 + 3000 + 1500 + 31300) - 29800) + 0.025 * (0.31 * (31300 + 3000 + 1500 + 31300) -29800)
Profit = 8568 + (-1061) + (-225)
Profit = +7282 chips eller tilsvarende til 2.42bb 


ICM har den som et -0.05 fold, men jeg føler selv så top tungt som de her (og mange MTT's) er, så må ovenstående og den raw chip value vel være mere relevant? Eller er det virkelig et fold? Hvis det er et fold, ved hvilket punkt (+Chip ev) kan vi begynde at sige det er et jam? +9k? 


Btw hvis nogen leder efter MTT sparring, så er jeg altid frisk, ovenstående er det nørderi jeg bruger mine timer på, i et forsøg på at blive bedre til MTT's. EDIT: Skal siges jeg først lige fra d. 1/2 er gået igang med at nørde MTT's igen, så er meget grøn på en del spots, men arbejder hårdt på at få det lært. 

Jeg læste ikke det hele, men jeg tror du begår en fejl, hvis du vil beregne ss for et call som 25% + 7%. Hvis du mener btn's call er uafhængigt af bb's call, så bør du beregne det som ss(for ikke at blive called): 0,93*0,75= 0,6975

 

Jeg regner ikke meget poker, - nok derfor jeg ikke er vindende - men ret overbevist om, at du ellers ryger ud i den klassiske "hvad er ss for at slå en sekser, hvis du kaster 6 terninger?"

moktar skrev:

Jeg læste ikke det hele, men jeg tror du begår en fejl, hvis du vil beregne ss for et call som 25% + 7%. Hvis du mener btn's call er uafhængigt af bb's call, så bør du beregne det som ss(for ikke at blive called): 0,93*0,75= 0,6975

 

Jeg regner ikke meget poker, - nok derfor jeg ikke er vindende - men ret overbevist om, at du ellers ryger ud i den klassiske "hvad er ss for at slå en sekser, hvis du kaster 6 terninger?"

 

Btn's call er ikke uafhængigt af BB's call, antager vi at BB kalder, så vil Btn's call være markant mindre end 25%. 

Det sagt ved jeg ikke om det så skal opstilles så formlen tilpasses det? altså de 7% af tiden BB kalder, skal vi adjust Btn's range og have en ny beregning?. 

Det er alt sammen ret nyt for mig, så jeg er dog på ingen måde sikker, jeg hijackede formlen direkte fra Jonathan Little, og har så bare leget med den, så valgte at stole på at det var en reliable formel. 

Hvis den ændrer sig, hvis bb caller skal du over i en helt anden udregning. Uanset hvad skal dine sandsynligheder beregnes med multiplikation, ikke med addition. Ellers ville sandsynligheden for at slå en sekser med 6 terninger være 1.

moktar skrev:

Hvis den ændrer sig, hvis bb caller skal du over i en helt anden udregning. Uanset hvad skal dine sandsynligheder beregnes med multiplikation, ikke med addition. Ellers ville sandsynligheden for at slå en sekser med 6 terninger være 1.

 

 Så det burde hedde 

Chance for begge folder = (1-0.07) * (1-0.25) 
Chance for begge folder = 0.93 * 0.75 
Chance for begge folder = 0.6975 ? 

Hvilket jo naturligvis kun gør situationen bedre, om end forskellen er enormt marginal. 

Men det ændre vel hele formlen, fordi lige nu er den lidt sat op til ''both fold'' / ''both call'' - Ift hvad chips vi trækker fra, hvor den nok skal nuanceres en del, for at tage højde for de forskellige scenarios. Omend så tænker jeg ikke det nogensinde bliver værre for os, fordi skal vi ud i at regne i 1 caller 1 fold, så vil vores chips ev jo kun blive bedre, da vi nu tager udgangspunkt i worst case scenario i chips lost. 

Incrazy skrev:

 

 Så det burde hedde 

Chance for begge folder = (1-0.07) * (1-0.25) 
Chance for begge folder = 0.93 * 0.75 
Chance for begge folder = 0.6975 ? 

Hvilket jo naturligvis kun gør situationen bedre, om end forskellen er enormt marginal. 

Men det ændre vel hele formlen, fordi lige nu er den lidt sat op til ''both fold'' / ''both call'' - Ift hvad chips vi trækker fra, hvor den nok skal nuanceres en del, for at tage højde for de forskellige scenarios. Omend så tænker jeg ikke det nogensinde bliver værre for os, fordi skal vi ud i at regne i 1 caller 1 fold, så vil vores chips ev jo kun blive bedre, da vi nu tager udgangspunkt i worst case scenario i chips lost. 

 

 

Der må du få nogle mere pokerstærke indover end mig for at vurdere det pokermæssige, men jeg vil påstå det er den korrekte beregning af at begge folder. Hvis du vil lave den fulde beregning må du regne ss for de 4 mulige scenarier: FF (69,75%), CC (?), CF (?), FC (?) vil jeg mene.

Uden sådan for alvor at kigge matematikken efter i sømmene, så er jeg ikke glad for de antagelser du laver.

 

Du antager at Button åbner 50% og kalder 16%. Hvor kommer de tal fra? Button ved vel godt at han ikke bør åbne så light, når der sidder en shortstack i blinds, eller alternativt at han bør kalde en meget højere%?

 

Du nævner at det er 2 recs og 2 regs? Hvem er hvem? Tænker det er enormt relevant i forhold til netop et spot som det her, hvor vi overvejer at afvige fra et simpelt fold pga. et bestemt leak hos "popuationen"?

 

Umiddelbart vil det ikke være et play jeg laver uden en god fornemmelse eller en note på button.